- А так ли плоха челка в iPhone? Мне она нравится
- Из-за челки iPhone узнаваем
- Челка не мешает просмотру контента
- А есть ли альтернативы челке в iPhone?
- Лонгриды для вас
- Кривые Безье
- Виды кривых Безье
- Математика
- Рисование «де Кастельжо»
- Постигая кривые Безье
- Кривая Безье первого порядка
- Кривые Безье второго порядка и больше
- Квадратичная кривая
- Рекурсивность кривых Безье
- Кубическая кривая
- Зачем все это нужно?
А так ли плоха челка в iPhone? Мне она нравится
Судя по тому, что о ней пишут и говорят, «челку» в айфонах мало кто любит. С того дня, когда она украсила фронтальную поверхность iPhone X, про неё не было сказано ни одного доброго слова. Иногда её защищают; мол, она необходима, иначе на экране, занявшем всю лицевую сторону смартфона, не разместишь все эти камеры, микрофоны и датчики. По общему мнению, её нужно убрать, превратить в крошечное отверстие, выдавить её содержимое в выступ над верхней гранью iPhone 13. На самом деле, в глубине души, мы её любим. Мы к ней привыкли, не обращаем на неё внимания, но когда её не станет, нам её будет не хватать.
iPhone без «челки» выглядит пустовато, не считаете?
Юбилейный iPhone X разрабатывали с особой тщательностью. В дизайне iPhone X не было ничего случайного – ни линии, ни закругления, ни выступа на корпусе. Вырез в верхней части экрана, позже названный «челкой», тем более не мог быть случайным. Этот вырез не мог не вызывать раздражения, но это их не остановило. iPhone X ругали, высмеивали, что только о нем не писали, но раскупали этот смартфон стремительно. Ни челка, ни высокая цена, ни беспрецедентная сложность, ни стоимость его ремонта этому не мешали. А в 2018 году челка даже вошла в моду. Такая поддержка Apple была неприятна, и мода сошла на нет. А что может быть хорошего в выемке из экрана?
Из-за челки iPhone узнаваем
Если вам кажется, что узнаваемость модели не имеет никакого значения, вы ошибаетесь. Устройства, у которых нет индивидуальности, хуже продаются. Ими не гордятся. За них не платят премиальную цену, а iPhone разрабатывают долго и тщательно, и дешевыми они просто не могут быть. Яблочко на тыльной стороне выделяло бы iPhone в толпе, но обычно его скрывает чехол или бампер.
До оккупации всей фронтальной поверхности экраном, iPhone был узнаваем. Кнопка Home, скупой как ни у кого другого экстерьер – с узнаваемостью не было проблем. Занять всю фронтальную поверхность экрану не дали, иначе пользователи лишились бы фронтальной камеры, микрофона и всех других сенсоров. Без них iPhone утратил бы свои магические способности, и был бы никому не интересен. Технический анклав пытались разместить в здесь и там, но вырез оказался лучшим решением. С индивидуальностью у iPhone все хорошо. Размеры камер уменьшаются, сенсоры скоро можно будет размещать под экраном ценой приемлемых затрат, челка станет ненужна. И Apple придется искать новое лицо iPhone.
Если выключить экран, с виду будет как рядовой Android-телефон
Челка не мешает просмотру контента
На самом деле в первые минуты, часы, а то и дни обладания смартфоном с челкой она отвлекает и даже раздражает. Но достаточно скоро её перестают замечать. Спокойно лазят в браузере, читают Твиттер или общаются в нашем Телеграм-чате. В Apple задолго до презентации iPhone X набрали статистику по этому вопросу, она вполне благоприятная. Проводили опыты над людьми. Над сотрудниками Apple из разных подразделений. Я не знаю ни одного челкофоба, но говорят, люди, которых выемка в верхней части экрана iPhone не перестает раздражать и через несколько лет, существуют.
Болезненнее всего вырезка в экране должна была обойтись iOS-разработчикам. Этого постарались не допустить, все необходимые действия для адаптации к челке были педантично расписаны. Работа с инородными вкраплениями в экранное пространство – не место для творческих поисков. Сообщений о жертвах не было. Судя по тому, с чем сталкиваются другие разработчики смартфонов, пытающиеся найти свой собственный путь, iOS-разработчикам повезло. С челкой серьезных проблем нет.
А есть ли альтернативы челке в iPhone?
Apple могла бы не обращать внимания на любовь пользователей к большим экранам во всю фронтальную поверхность и не следовать моде. Аналитики Apple по продажам просчитали последствия такого решения, они были бы неутешительными. К тому же у Apple были очень интересные наработки в области распознавания лиц и приближался юбилей. Технический анклав можно было бы разместить в верхней рамке – сделав её достаточно толстой для этого.
В iPad Pro и iPad Air четвертого поколения Apple так и сделала, но с iPhone это не прошло бы – экраны в iPhone слишком небольшие, выглядело бы это очень так себе. Решили, что все необходимые сенсоры соберут в выемке в верхней части экрана.
ZTE Axon 20 5G, все датчики спрятаны под экран
У конкурентов для тех же целей используются разные решения. Например, размещают сенсоры в отверстии где-нибудь на экране. Просмотру видео несколько потерянных пикселей особо не мешают, экран кажется абсолютно свободным, но в Apple решили не идти по этому пути. Выдвигающиеся элементы (как в Vivo Nex или в Oppo Find X) это сложно, ненадежно и не в стиле Apple. Не лаконично.
Попытки убрать все сенсоры под экран, как в ZTE Axon 20 5G, пока неубедительны и преждевременны. В Apple занимаются подэкранными сенсорами, но пока не считают их соответствующими стандартам.
Новости, статьи и анонсы публикаций
Свободное общение и обсуждение материалов
Лонгриды для вас
Допустим, вы точно решили приобрести iPhone 12 Mini. Это отличный выбор, но… Рассказываем, чем хорош этот компактный смартфон. И как одним своим минусом он может подпортить вам весь кайф от использования
Apple выпустила уже четвёртую бета-версию iOS 14.7, но обновление пока не содержит ни одной новой функции. Впрочем, время для тестирования ещё есть, поэтому не теряем надежды
QR-код можно сделать прямо на iPhone. Есть специальное приложение, которое позволяет привязать QR-код практически к любой ситуации — от подключения к сети Wi-Fi до сохранения визитной карточки другого пользователя
«С челкой айфон узнаваем» — вы из тех людей которые считает айфон статусной вещью?)
Источник
Кривые Безье
Материал на этой странице устарел, поэтому скрыт из оглавления сайта.
Более новая информация по этой теме находится на странице https://learn.javascript.ru/bezier-curve.
Кривые Безье используются в компьютерной графике для рисования плавных изгибов, в CSS-анимации и много где ещё.
Несмотря на «умное» название – это очень простая штука.
В принципе, можно создавать анимацию и без знания кривых Безье, но стоит один раз изучить эту тему хотя бы для того, чтобы в дальнейшем с комфортом пользоваться этим замечательным инструментом. Тем более что в мире векторной графики и продвинутых анимаций без них никак.
Виды кривых Безье
Кривая Безье задаётся опорными точками.
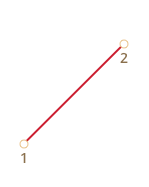
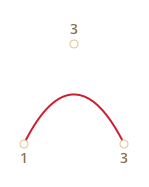
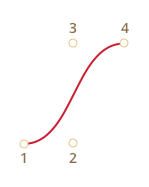
Их может быть две, три, четыре или больше. Например:
По четырём точкам:
Если вы посмотрите внимательно на эти кривые, то «на глазок» заметите:
Точки не всегда на кривой. Это совершенно нормально, как именно строится кривая мы рассмотрим чуть позже.
Степень кривой равна числу точек минус один. Для двух точек – это линейная кривая (т.е. прямая), для трёх точек – квадратическая кривая (парабола), для четырёх – кубическая.
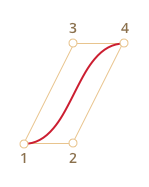
Кривая всегда находится внутри выпуклой оболочки, образованной опорными точками:
Благодаря последнему свойству в компьютерной графике можно оптимизировать проверку пересечений двух кривых. Если их выпуклые оболочки не пересекаются, то и кривые тоже не пересекутся.
Основная ценность кривых Безье для рисования – в том, что, двигая точки, кривую можно менять, причём кривая при этом меняется интуитивно понятным образом.
Попробуйте двигать точки мышью в примере ниже:
Как можно заметить, кривая натянута по касательным 1 → 2 и 3 → 4.
После небольшой практики становится понятно, как расположить точки, чтобы получить нужную форму. А, соединяя несколько кривых, можно получить практически что угодно.
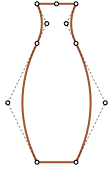
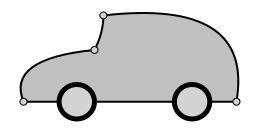
Вот некоторые примеры:
Математика
У кривых Безье есть математическая формула.
Как мы увидим далее, для пользования кривыми Безье знать её нет особенной необходимости, но для полноты картины – вот она.
Координаты кривой описываются в зависимости от параметра t⋲[0,1]
Для четырёх точек:
Вместо Pi нужно подставить координаты i-й опорной точки (xi, yi) .
Эти уравнения векторные, то есть для каждой из координат:
Вместо x1, y1, x2, y2, x3, y3 подставляются координаты трёх опорных точек, и в то время как t пробегает множество от 0 до 1 , соответствующие значения (x, y) как раз и образуют кривую.
Впрочем, это чересчур наукообразно, не очень понятно, почему кривые именно такие, и как зависят от опорных точек. С этим нам поможет разобраться другой, более наглядный алгоритм.
Рисование «де Кастельжо»
Метод де Кастельжо идентичен математическому определению кривой и наглядно показывает, как она строится.
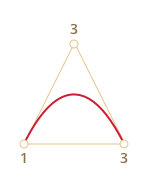
Посмотрим его на примере трёх точек (точки можно двигать). Нажатие на кнопку «play» запустит демонстрацию.
Алгоритм построения кривой по «методу де Кастельжо»:
Рисуем опорные точки. В примере выше это 1 , 2 , 3 .
Строятся отрезки между опорными точками 1 → 2 → 3. На рисунке выше они коричневые .
Параметр t пробегает значения от 0 до 1 . В примере выше использован шаг 0.05 , т.е. в цикле 0, 0.05, 0.1, 0.15, . 0.95, 1 .
Для каждого из этих значений t :
На каждом из коричневых отрезков берётся точка, находящаяся от начала на расстоянии от 0 до t пропорционально длине. Так как коричневых отрезков – два, то и точек две штуки.
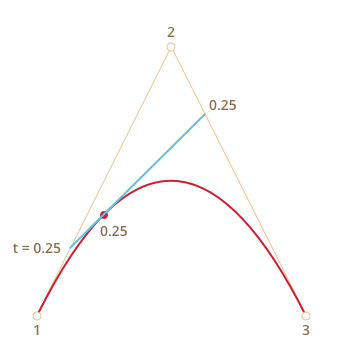
Например, при t=0 – точки будут в начале, при t=0.25 – на расстоянии в 25% от начала отрезка, при t=0.5 – 50%(на середине), при t=1 – в конце отрезков.
Эти точки соединяются. На рисунке ниже соединяющий их отрезок изображён синим .
| При t=0.25 | При t=0.5 |
|---|---|
 | 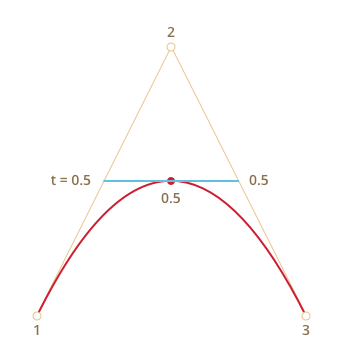 |
- Точки по порядку соединяются отрезками: 1 → 2, 2 → 3, 3 → 4. Получается три коричневых отрезка.
- На отрезках берутся точки, соответствующие текущему t , соединяются. Получается два зелёных отрезка .
- На этих отрезках берутся точки, соответствующие текущему t , соединяются. Получается один синий отрезок .
- На синем отрезке берётся точка, соответствующая текущему t . При запуске примера выше она красная .
- Эти точки описывают кривую.
- первая контрольная точка — P0 имеет координаты (0; 0),
- вторая (и последняя) – P1 – (5; 0).
- P0 – начало;
- P2 – конец;
- P1 – вспомогательная точка, определяющая изгиб кривой.
- Строим кривые первого порядка P0-P1, P1-P2, P2-P3
- Находим на них соответствующие t точки Q0, Q1, Q2
- Строим кривые первого порядка Q0-Q1 и Q1-Q2
- Находим на них соответствующие t точки R0 и R1
- Строим кривую первого порядка R0-R1
- Находим на ней точку, соответствующую t .
На получившемся отрезке берётся точка на расстоянии, соответствующем t . То есть, для t=0.25 (первый рисунок) получаем точку в конце первой четверти отрезка, для t=0.5 (второй рисунок) – в середине отрезка. На рисунках выше эта точка отмечена красным .
По мере того как t пробегает последовательность от 0 до 1 , каждое значение t добавляет к красной кривой точку. Совокупность таких точек для всех значений t образуют кривую Безье.
Это был процесс для построения по трём точкам. Но то же самое происходит и с четырьмя точками.
Демо для четырёх точек (точки можно двигать):
Этот алгоритм рекурсивен. Для каждого t из интервала от 0 до 1 по этому правилу, соединяя точки на соответствующем расстоянии, из 4 отрезков делается 3, затем из 3 так же делается 2, затем из 2 отрезков – точка, описывающая кривую для данного значения t .
Нажмите на кнопку «play» в примере выше, чтобы увидеть это в действии.
Источник
Постигая кривые Безье
Кривые Безье — это способ определения кривой по опорным точкам.
Для наглядности можно рассматривать их как график передвижения точки от начала до конца маршрута в зависимости от времени движения.
Время изменяется от 0 до 1 (до 100%). То есть мы изначально знаем время, за которое нужно переместиться из начальной точки (P0) в конечную (Pn) (конкретная величина не имеет значения). На основании этого времени можно вычислить точную траекторию — по формулам.
Берем все время за 100% (или за единицу). В момент 0 (0%) точка находится в точке P0, в момент 1 (100%) – в точке Pn. Положение точки в любой момент между этими моментами можно вычислить по формуле.
Порядок кривой всегда на 1 меньше количества контрольных точек. Рассмотрим построение пошагово, начиная с самой простой кривой.
Кривая Безье первого порядка
Простейшая кривая Безье — это обычная линия. Порядок первый – значит, контрольных точек две. Ее академическое уравнение выглядит так:
А график — вот так:
Разберем на простейшем примере. Пусть:
Сразу же проверим формулу.
При t = 0 (в начальный момент времени) должна получиться точка P0, а при t = 1 должна получиться точка P1.
А теперь найдем несколько точек между началом и концом. Тут используется сложение и умножение векторов, но в данном случае все интуитивно понятно:
Все полученные точки лежат на одной прямой – это и есть кривая Безье первого порядка.
Время идет, точка движется от старта к финишу. И в любой момент времени мы точно знаем, где она находится.
Кривые Безье второго порядка и больше
В определении кривых Безье выше первого порядка кроме начала и конца появляются дополнительные опорные точки, смысл которых сложно понять с первого захода.
Непосредственно через них кривая не проходит, так зачем же они нужны?
На самом деле эти точки определяют направление движения (направление изгиба кривой) и крутизну этого изгиба.
Квадратичная кривая
Кривая Безье второго порядка, или квадратичная, задается тремя контрольными точками:
Маленький спойлер: кривая Безье второго порядка имеет форму параболы (не обязательно симметричной).
Формула у нее вот такая:
B(t) = (1 — t) 2 *P0 + 2t*(1 — t)*P1 + t 2 *P2
Проверим, что в начале и конце движения мы окажемся в точках P0 и P2 соответственно:
Найдем, где будет точка через половину времени t (0.5):
B(0.5) = 0.25*P0 + 0.5*P1 + 0.25*P2 = (-0.25; 0) + (0; 1) + (0.25; 0) = (0; 1)
То есть на половине временного интервала мы окажемся в точке (0; 1) .
Если найти еще несколько точек, вырисуется ровная парабола. Так, в общем, и было задумано для простоты вычислений и визуальной ясности.
Рекурсивность кривых Безье
Волшебство кривых Безье заключается в том, что они рекурсивны. То есть умея строить кривую первого порядка, мы можем построить и квадратичную кривую, даже не зная ее формулы.
Вернемся к предыдущему примеру:
Предположим, что мы не знаем, как построить кривую второго порядка между P0 и P2. Но мы можем построить простейшую кривую первого порядка между P0 и P1, а также между P1 и P2, пользуясь формулой:
Для каждого момента времени мы можем найти положение точки на каждой из этих кривых.
Например, в момент времени 0.25 соответствующие точки Q0 и Q1 будут в таких позициях:
Между этими точками тоже можно построить кривую первого порядка.
Магия заключается в том, что точка на этой кривой в момент времени t = 0.25 соответствует точке на искомой кривой второго порядка в этот же момент времени.
Распишем чуть подробнее.
Мы хотим найти точку на кривой второго порядка P0-P11-P2 в момент времени t .
Искомая точка – это точка на кривой Q0-Q1, соответствующая моменту времени t .
Этот рекурсивный алгоритм построения кривой Безье носит имя Поля де Кастельжо.
Кубическая кривая
Кривая Безье третьего порядка, или кубическая кривая, определяется уже четырьмя опорными точками – началом, концом и двумя вспомогательными, через которые она не будет непосредственно проходить.
Две вспомогательные точки снова определяют направление и крутизну изгибов кривой.
Формула кубической кривой еще сложнее:
B(t) = (1 — t) 3 *P0 + 3t*(1-t) 2 *P1 + 3t 2 *(1 — t)*P2 + t 3 *P3
Вы можете попробовать эту кривую рассчитать самостоятельно.
Обратите внимание, ее тоже можно получить рекурсивно!
Найти точку кривой третьего порядка в момент времени t можно по следующему алгоритму:
Зачем все это нужно?
Круто, теперь мы умеем строить кривые Безье любого порядка, но зачем нам это нужно? Каково практическое применение этих построений?
Кривые Безье используются в описаниях шрифтов TrueType, в SVG, GIMP и других графических форматах, в 3D-графике. Они используются даже в CSS для описания плавности анимации.
Источник