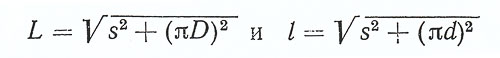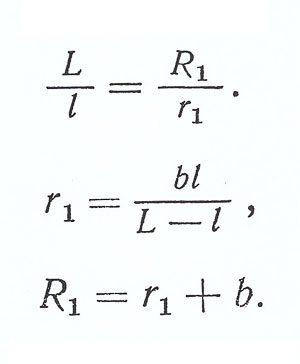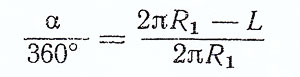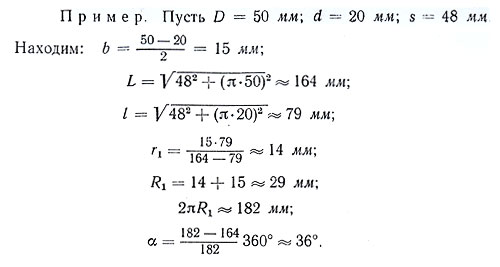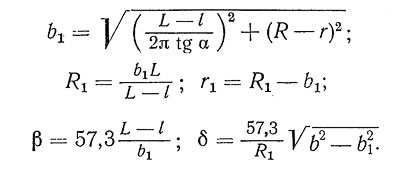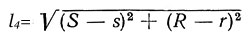Развертка шнека для айфона

Расчет шнека (развертка витка)

Поверхность витков шнека изготовленных из листовых заготовок близка к поверхности прямого кольцевого геликоида (или, иначе – винтового коноида). Строго математически поверхность геликоида, не может быть развернута в плоскость. Это означает и обратное — .

. теоретически из плоской заготовки нельзя получить виток геликоида.

Но на практике все сплошь и рядом изготавливают рабочие поверхности шнеков из металлического листа! Листовая заготовка при деформации в виток подвергается не только изгибу, но и вытяжке и сжатию (формовке). При этом локально изменяется начальная толщина листа заготовки! Классическая теория поверхностей, конечно, не предполагает деформационного растяжения или сжатия объектов исследования.

Далее рассмотрен широко применяющийся на практике приближенный расчет развертки витка шнека в виде сектора концентрического кольца с простым выводом всех формул алгоритма. Быстро и удобно выполнить расчет шнека (точнее – развертки витка шнека) призвана помочь небольшая программа, реализованная в Excel.

Расчет в Excel развертки витка шнека.

Рассмотрим виток шнека.

Длина наружной винтовой линии витка шнека по теореме Пифагора:

L=((π*D) 2 +t 2 ) 0,5 (1)

Аналогично длина внутренней винтовой линии витка шнека:

l=((π*d) 2 +t 2 ) 0,5 (2)

Высота витка шнека:

a=(D— d)/2 (3)

Перейдем к рассмотрению развертки витка шнека.

Три следующих формулы отражают зависимости между пространственным витком и плоской разверткой. (Углы в расчетах – в радианах!)

Длина наружной дуги заготовки должна быть равна длине наружной винтовой линии витка:

L=α*D₀/2 (4)

Длина внутренней дуги заготовки должна быть равна длине внутренней винтовой линии витка шнека:

l=α*d₀/2 (5)

Ширина кольцевого сектора заготовки должна быть равна высоте витка шнека:

a=(D₀— d₀)/2 (6)

Вычтем уравнение (5) из выражения (4), заменим часть выражения зависимостью (6) и выразим угол кольцевого тела развертки:

L— l=α *(D₀— d₀)/2=α *a

α=(L— l)/a (7)

Зная угол α из выражений (4) и (5) находим диаметры развертки:

D₀=2*L/α (8)

d₀=2*l/α (9)

Угол выреза в развертке:

β=2*π— α (10)

Размер вырезов по наружному и внутреннему диаметрам развертки:

B= D₀*sin (β/2) (11)

b= d₀*sin(β/2) (12)

В заключение для справки вычислим массу заготовки витка шнека:

G=s*(π/4)*(D₀ 2 — d₀ 2 )/(2*π)*α*ρ (13)

На размещенном ниже скриншоте показан пример расчета в Excel, реализующего рассмотренный несложный алгоритм.

Замечания.

Напоминаю, что выполненный расчет витка шнека — приближенный! Попытки его улучшить чаще всего не имеют ни теоретического, ни практического смысла, так как точность поверхности витка зависит от способа его формообразования.

При необходимости получения высокой точности размеры развертки заготовки можно попытаться скорректировать для каждого конкретного случая индивидуально по результатам экспериментальных замеров. Иногда рационально ввести дополнительно механическую обработку диаметров на токарном станке после формовки и сварки.

Какова же точность развертки, полученной по представленной программе?

Виток винтового коноида с параметрами, заданными в качестве исходных данных (смотри скриншот выше), имеет массу 191 грамм по данным моделирования в одной из CAD-программ. Масса развертки витка по программе в Excel – почти 197 грамм. Разница — 3%. Развертка больше! Возможно, диаметры стоит уменьшить? Не стоит торопиться делать выводы. Если толщина листа в рассматриваемом примере будет меньше всего лишь на 0,05 мм, массы заготовки и теоретического витка станут равными.

По неподтвержденным данным размеры разверток, полученные по рассмотренным формулам, больше реально требуемых размеров на 1,4…1,8%.

Толщина листа заготовки витка шнека (s) и плотность материала (ρ) участвуют лишь в расчете массы (G), поэтому ввод этих значений в исходные данные при расчете только геометрических размеров развертки не является необходимым.

Прошу уважающих труд автора и желающих получать информацию о новых программах на сайте скачивать файл с программой расчетов после подписки на анонсы статей!

Ссылка на скачивание файла с программой расчета: raschet-razvertki-vitka-shneka-v-excel (xls 171KB).

В CAD SolidWorks есть интересное приложение BLANKWORKS (www.intersed.kiev.ua/blankworks):

«BLANKWORKS рассчитывает точную форму заготовки для простых и сложных деталей. В отличие от большинства подобных систем, BLANKWORKS способен работать с деталями, изготавливаемыми частично штамповкой с объемной деформацией, а частично гибкой. Расчет заготовки занимает лишь несколько минут и дает результат, имеющий точность, достаточную для предварительной оценки технологичности, оценки расхода и оптимизации раскроя материала. BLANKWORKS отображает также эпюру степени утонения материала.»

Интересно было бы услышать отзывы пользователей этой системы и сравнить результаты расчетов и факты практики.

Источник

Развертка поверхности витка шнека

Развертка поверхности прямого кольцевого винтового коноида

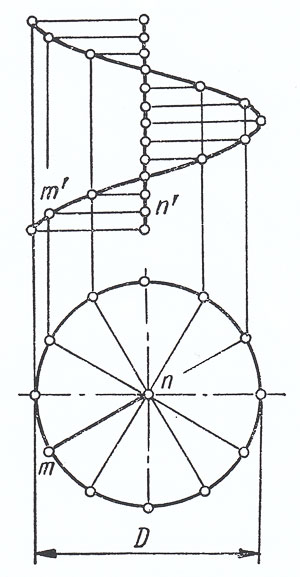
Рассмотрим прямой геликоид, который образован движением прямолинейной образующей NM по двум направляющим (цилиндрической винтовой линии и ее оси), причем во всех положениях образующая составляет с осью прямой угол и остается параллельной плоскости параллелизма (на рис.1 — горизонтальной плоскости).

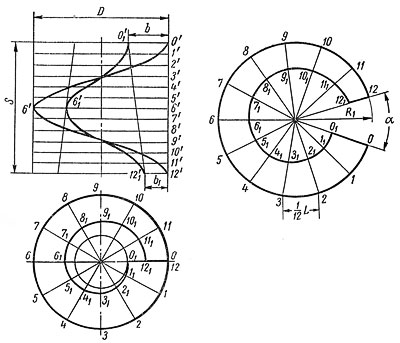
Приближенная развертка одного витка представляет собой часть плоского кольца, заключенного между двумя концентрическими дугами (рис 2).

Рисунок 1

Рисунок 2

Длина L большой дуги равна длине одного витка внешней винтовой линии; длина l меньшей дуги равна длине витка внутренней винтовой линии. Радиусы дуг R 1 и r 1 и угол выреза α могут быть определены графически и аналитически.

Аналитический способ

Обозначим ширину винтовой поверхности b, причём b = D-d/2

Формула 1

Так как винтовые линии развертываются в две концентрические дуги при одном и том же центральном угле, а такие дуги относятся друг к другу как радиусы, то

Формула 2

Угол выреза α определяется из пропорции:

Формула 3

Графический способ

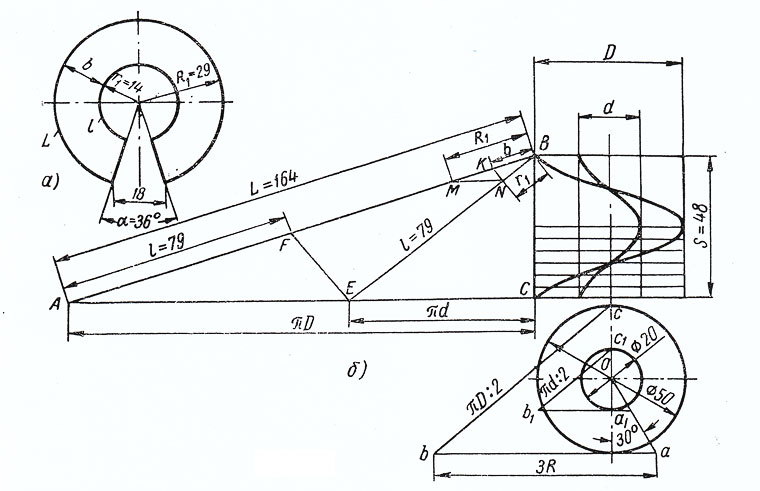
Величины r 1, R 1 и α могут быть определены графическим построением (2 рис.б).
Строим прямоугольные треугольники АВС и ЕВС, у которых катет ВС = s = 48 мм, а катеты АС и ЕС равны длинам окружностей πD и πd. Величины πD и πd вычисляются или определяются следующим построением: проводим прямую Оа (б — правый нижний рисунок) под углом 30° к вертикальному диаметру до пересечения в точке а с касательной, проходящей через нижний конец того же диаметра. От точки а откладываем на касательной длину трех радиусов и полученную точка b соединяем с верхним концом диаметра. Отрезок bc равен половине длины окружности.

Гипотенузы построенных треугольников выражают длины развернутых винтовых линий L и l.
Для построений длины r 1 откладываем на АВ от точки А отрезок AF = l и от точки В отрезок ВК = b. Соединяем точки F и Е прямой EF и через точку К проводим прямую KN || EF до пересечения с BE в точке N.
Тогда отрезок BN = r 1 = 14 мм. (Действительно, из подобия треугольников BEF и BNK следует, что BN/BE = BK/BF. Но BN = r 1, BE = l, BK = b; BF = L — l. Отсюда r 1 = bl/(L — l).

Радиус R 1 = r 1 + b = 14 + 15 = 29 мм. Его можно найти и непосредственно построением, если через точку N провести прямую NM || AC до пересечения с АВ. Тогда отрезок ВМ = R 1 = 29 мм.

Для построения угла выреза α откладываем на окружности радиуса R 1 разность между длиной окружности 2π R 1 и длиной дуги L, равную 18 мм, и концы отложенной дуги соединяем с центром.

При больших значениях D, d и s выполнение вышеописанных построений в натуральную величину затруднительно. В таком случае следует пользоваться аналитическим способом или выполнять построения в уменьшенном масштабе, что снижает точность результата.

Выкроив из листа требуемое количество отдельных витков, можно образовать из них винтовую поверхность. Для присоединения витков к поверхности цилиндра диаметром d, на последней прочерчивают винтовую линию заданного шага s. Способы присоединения и соединения витков зависят от принятой технологии.

Развертка поверхности прямого винтового коноида переменной ширины

В данном случае внутренняя направляющая винтовая линия расположена на конусе, ширина поверхности коноида непрерывно изменяемая от максимальной величины b до минимальной b1.

Рисунок 3

Горизонтальная проекция внешней винтовой линии (цилиндрической ) является окружностью, а проекция внутренней винтовой линии (конической) представляет собой спираль Архимеда.

Для построения развертки определяют предварительно величины R 1 и α (формулы 1 — 3). Чертят окружность радиусом R 1 и наносят на ней центральный угол α. Полученную дугу, длина которой равна L, делят на несколько равных частей (на рис. 3 на 12) и проводят радиусы через точки деления. На радиусах откладывают последовательно длины отрезков 0 — 01; 1 — 11; 2 — 22 и т.д., взятые с горизонтальной проекции, где они изображаются в натуральную величину. Таким образом, получают ряд точек — 11; 21; 31;…121, соединяемых плавной кривой.

Развертка поверхности косого винтового геликоида

В данном случае, каждая образующая поверхности остается параллельной соответствующей образующей некоторого соосного конуса вращения с углом при вершине равным 2α, который называется направляющим конусом.

Рисунок 4

Графический способ

Для построения развертки одного витка данной поверхности разбивают горизонтальную проекцию на равные части (например, на 12) и принимаю каждую из них за равнобокую трапецию.

Боковые стороны всех трапеций равны. Натуральную величину их дает фронтальная проекция 0′ — 0’1 = b — ширине поверхности.

Величина b может быть вычислена по формуле b = R — r/sinα.

Две другие стороны, например 0 — 1 и 01 — 11, равны соответственно 1/12 L и 1/12 l, где L и l — длины одного оборота внешней и внутренней винтовых линий. Для построения трапеции необходимо знать еще длину её диагонали, например 0 — 11. Определив любым известным способом истинную длину диагонали по её проекциям (011 и 0’1’1), строим приближенную развертку, как ряд примыкающих один к другому равных треугольников (рис. 4, б). Каждый треугольник строится по трем известным сторонам. Затем вершины треугольников обводятся плавной кривой.

Аналитический способ

Основан на изгибании поверхности косого геликоида на однополостный гиперболоид вращения, поверхность которого затем заменяется усеченным круговым конусом. Размеры развертки одного витка (рис. 4, в) определяется по формулам:

Формула 4

Развертка винтовой поверхности переменного шага

В рассмотренных выше примерах внешняя и внутренняя винтовые направляющие данных поверхностей имели один и тот же шаг. Для увеличения угла подъема внешней винтовой направляющей увеличивают её шаг.
Таким образом, винтовые направляющие имеют в этом случае разные шаги S и s, и сама поверхность называется винтовой поверхностью с переменным шагом.

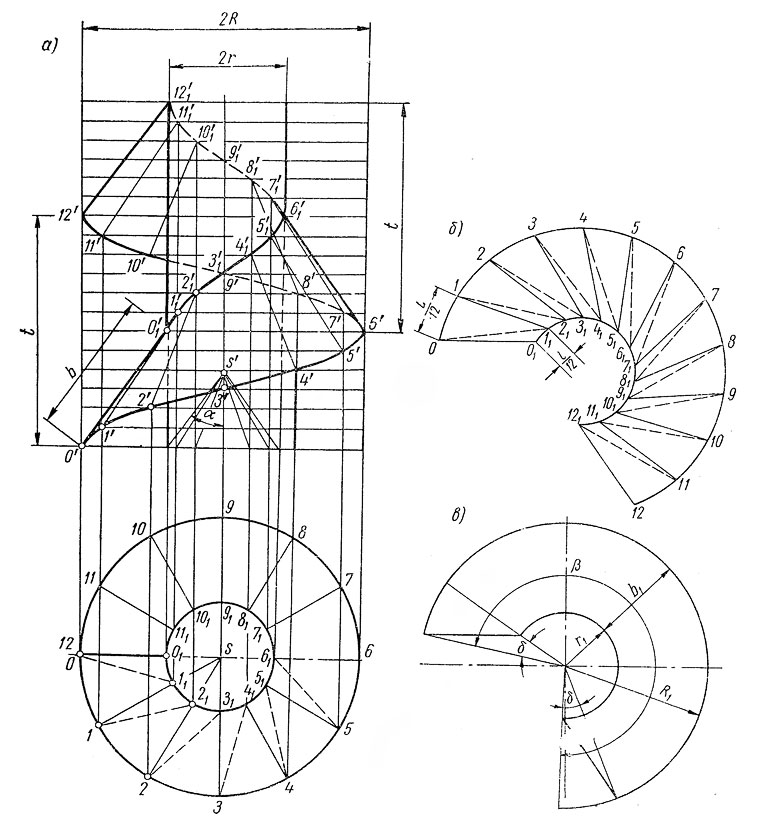
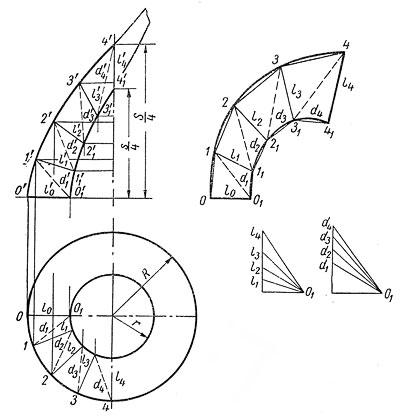
На рис. 5 даны проекции ¼ полного оборота такой винтовой поверхности. Один конец образующей движется по винтовой линии шага S и радиуса R, а другой — по винтовой линии шага s и радиуса r.

При этом угол, под которым образующая пересекает вертикальную ось, уже не остается постоянным и отрезки образующей, заключенные между направляющими так же не равны между собой. Минимальная длина этих отрезков l0 = 001 = R — r; максимальная (l4) равна гипотенузе прямоугольного треугольника, одним катетом которого является фронтальная проекция 4′ — 4’1, а другим — горизонтальная проекция того же отрезка, т.е.

Рисунок 5

Построение приближенной развертки для ¼ полного витка произведено тем же способом, что и в предыдущем примере, но в данном случае приходится определять истинную длину каждой боковой стороны заменяемых трапециями отсеков поверхности и каждой диагонали. Это выполнено на рисунке 5 построением прямоугольных треугольников по известным из начертательной геометрии приемам.

Что касается двух других сторон всех отсеков, то они, как и в предыдущем примере, равны L/n и l/n, где n — принятое число делений одного оборота винтовых направляющих (в данном случае n = 16). Величины L и l определяются как указано выше (по формулам 2).

По материалам:
«Технические развертки изделий из листового металла» Н.Н. Высоцкая 1968 г. «Машиностроение»

Источник