Set string java android

Набор данных интерфейса Set

Реализация интерфейса Set представляет собой неупорядоченную коллекцию, которая не может содержать дублирующие данные.

Интерфейс Set включает следующие методы :

Метод	Описание
add(Object o)	Добавление элемента в коллекцию, если он отсутствует. Возвращает true, если элемент добавлен.
addAll(Collection c)	Добавление элементов коллекции, если они отсутствуют.
clear()	Очистка коллекции.
contains(Object o)	Проверка присутствия элемента в наборе. Возвращает true, если элемент найден.
containsAll(Collection c)	Проверка присутсвия коллекции в наборе. Возвращает true, если все элементы содержатся в наборе.
equals(Object o)	Проверка на равенство.
hashCode()	Получение hashCode набора.
isEmpty()	Проверка наличия элементов. Возвращает true если в коллекции нет ни одного элемента.
iterator()	Функция получения итератора коллекции.
remove(Object o)	Удаление элемента из набора.
removeAll(Collection c)	Удаление из набора всех элементов переданной коллекции.
retainAll(Collection c)	Удаление элементов, не принадлежащих переданной коллекции.
size()	Количество элементов коллекции
toArray()	Преобразование набора в массив элементов.
toArray(T[] a)	Преобразование набора в массив элементов. В отличии от предыдущего метода, который возвращает массив объектов типа Object, данный метод возвращает массив объектов типа, переданного в параметре.

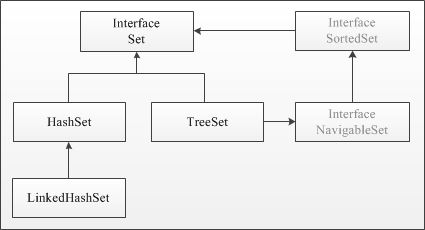
К семейству интерфейса Set относятся HashSet, TreeSet и LinkedHashSet. В множествах Set разные реализации используют разный порядок хранения элементов. В HashSet порядок элементов оптимизирован для быстрого поиска. В контейнере TreeSet объекты хранятся отсортированными по возрастанию. LinkedHashSet хранит элементы в порядке добавления.

Набор данных HashSet

Конструкторы HashSet :

Методы HashSet

• public int size()
• public boolean isEmpty()
• public boolean add(Object o)
• public boolean addAll(Collection c)
• public boolean remove(Object o)
• public boolean removeAll(Collection c)
• public boolean contains(Object o)
• public void clear()
• public Object clone()
• public Iterator iterator()
• public Object[] toArray()
• public boolean retainAll(Collection c)

HashSet содержит методы аналогично ArrayList. Исключением является метод add(Object o), который добавляет объект только в том случае, если он отсутствует. Если объект добавлен, то метод add возвращает значение — true, в противном случае false.

Пример использования HashSet :

В консоли мы должны увидеть только 4 записи. Следует отметить, что порядок добавления записей в набор будет непредсказуемым. HashSet использует хэширование для ускорения выборки.

Пример использования HashSet с целочисленными значениями. В набор добавляем значения от 0 до 9 из 25 возможных случайным образом выбранных значений — дублирование не будет.

Следует отметить, что реализация HashSet не синхронизируется. Если многократные потоки получают доступ к набору хеша одновременно, а один или несколько потоков должны изменять набор, то он должен быть синхронизирован внешне. Это лучше всего выполнить во время создания, чтобы предотвратить случайный несинхронизируемый доступ к набору :

Набор данных LinkedHashSet

Класс LinkedHashSet наследует HashSet, не добавляя никаких новых методов, и поддерживает связный список элементов набора в том порядке, в котором они вставлялись. Это позволяет организовать упорядоченную итерацию вставки в набор.

Также, как и HashSet, LinkedHashSet не синхронизируется. Поэтому при использовании данной реализации в приложении с множеством потоков, часть из которых может вносить изменения в набор, следует на этапе создания выполнить синхронизацию :

Набор данных TreeSet

Класс TreeSet создаёт коллекцию, которая для хранения элементов использует дерево. Объекты хранятся в отсортированном порядке по возрастанию.

Конструкторы TreeSet :

Методы TreeSet

• boolean add(Object o)
• boolean addAll(Collection c)
• Object ceiling(Object o)
• void clear()
• TreeSet clone()
• Comparator comparator()
• boolean contains(Object o)
• Iterator descendingIterator()
• NavigableSet descendingSet()
• Object first()
• Object floor(Object o)
• SortedSet headSet(E e)
• NavigableSet headSet(E e, boolean inclusive)
• Object higher(Object o)
• boolean isEmpty()
• Iterator iterator()
• E last()
• E lower(E e)
• E pollFirst()
• E pollLast()
• boolean remove(Object o)
• int size()
• Spliterator spliterator()
• NavigableSet subSet(E fromElement, boolean fromInclusive, E toElement, boolean toInclusive)
• SortedSet subSet(E fromElement, E toElement)
• SortedSet tailSet(E fromElement)
• NavigableSet tailSet(E fromElement, boolean inclusive)

В следующем измененном примере с использования TreeSet в консоль будут выведены значения в упорядоченном виде.

Источник

Множества: Set, HashSet, LinkedHashSet, TreeSet

HashSet, TreeSet и LinkedHashSet относятся к семейству Set. В множествах Set каждый элемент хранится только в одном экземпляре, а разные реализации Set используют разный порядок хранения элементов. В HashSet порядок элементов определяется по сложному алгоритму. Если порядок хранения для вас важен, используйте контейнер TreeSet, в котором объекты хранятся отсортированными по возрастанию в порядке сравнения или LinkedHashSet с хранением элементов в порядке добавления.

Множества часто используются для проверки принадлежности, чтобы вы могли легко проверить, принадлежит ли объект заданному множеству, поэтому на практике обычно выбирается реализация HashSet, оптимизированная для быстрого поиска.

В Android 11 (R) обещают добавить несколько перегруженных версий метода of(), которые являются частью Java 8.

HashSet

Название Hash. происходит от понятия хэш-функция. Хэш-функция — это функция, сужающая множество значений объекта до некоторого подмножества целых чисел. Класс Object имеет метод hashCode(), который используется классом HashSet для эффективного размещения объектов, заносимых в коллекцию. В классах объектов, заносимых в HashSet, этот метод должен быть переопределен (override).

Имеет два основных конструктора (аналогично ArrayList):

Методы

• public Iterator iterator()
• public int size()
• public boolean isEmpty()
• public boolean contains(Object o)
• public boolean add(Object o)
• public boolean addAll(Collection c)
• public Object[] toArray()
• public boolean remove(Object o)
• public boolean removeAll(Collection c)
• public boolean retainAll(Collection c) — (retain — сохранить). Выполняет операцию «пересечение множеств».
• public void clear()
• public Object clone()

Методы аналогичны методам ArrayList за исключением того, что метод add(Object o) добавляет объект в множество только в том случае, если его там нет. Возвращаемое методом значение — true, если объект добавлен, и false, если нет.

Перейдём к практике. Как это ни странно, но в жизни встречаются несколько Барсиков, Мурзиков и прочих Рыжиков. Несмотря на одинаковые имена, каждый кот неповторим. Надеюсь, с этим никто не спорит. Но пихать имена котов в множество HashSet не стоит, так как в множестве может храниться только одно имя и двух Мурзиков тут не записать. Другое дело — страны. Не может быть двух Франций, двух Англий, двух Россий (даже партия такая есть Единая Россия, впрочем мы отвлеклись).

Итак, создадим множество стран.

Нажав на кнопку, вы получите результат Размер HashSet = 4.

Даже если вы попытаетесь схитрить и дополнительно вставить строку countryHashSet.add(«Кот-Д’Ивуар»); после России, то всё-равно размер останется прежним.

Убедиться в этом можно, если вызвать метод iterator(), который позволяет получить всё множество элементов:

Несмотря на наше упрямство, мы видим только четыре добавленных элемента.

Стоит отметить, что порядок добавления стран во множество будет непредсказуемым. HashSet использует хэширование для ускорения выборки. Если вам нужно, чтобы результат был отсортирован, то пользуйтесь TreeSet.

Преобразовать в массив и вывести в ListView

Следующий пример — задел на будущее. Когда вы узнаете, что такое ListView, то вернитесь к этому уроку и узнайте, как сконвертировать множество в массив и вывести результат в компонент ListView (Список):

Продолжим опыты. Поработаем теперь с числами.

Здесь мы ещё раз убеждаемся, что повторное добавление числа не происходит. В цикле случайным образом выбирается число от 0 до 9 тысячу раз. Естественно, многие числа должны были повториться при таком сценарии, но во множество каждое число попадёт один раз.

При этом данные не сортируются, так как расположены как попало.

Специально для Android был разработан новый класс ArraySet, который более эффективен.

LinkedHashSet

Класс LinkedHashSet расширяет класс HashSet, не добавляя никаких новых методов. Класс поддерживает связный список элементов набора в том порядке, в котором они вставлялись. Это позволяет организовать упорядоченную итерацию вставки в набор.

TreeSet

Переделанный пример для вывода случайных чисел в отсортированном порядке. HashSet не может гарантировать, что данные будут отсортированы, так как работает по другому алгоритму. Если сортировка для вас важна, то используйте TreeSet.

Со строками это выглядит нагляднее:

Названия стран выведутся в алфавитном порядке.

Класс TreeSet создаёт коллекцию, которая для хранения элементов применяет дерево. Объекты сохраняются в отсортированном порядке по возрастанию.

SortedSet

В примере с TreeSet использовался интерфейс SortedSet, который позволяет сортировать элементы множества. По умолчанию сортировка производится привычным способом, но можно изменить это поведение через интерфейс Comparable.

Кроме стандартных методов Set у интерфейса есть свои методы.

• Comparator comparator()
• subSet(Object fromElement, Object toElement)
• tailSet(Object fromElement)
• headSet(Object toElement)
• Object first()
• Object last()

Источник

The Set Interface

A Set is a Collection that cannot contain duplicate elements. It models the mathematical set abstraction. The Set interface contains only methods inherited from Collection and adds the restriction that duplicate elements are prohibited. Set also adds a stronger contract on the behavior of the equals and hashCode operations, allowing Set instances to be compared meaningfully even if their implementation types differ. Two Set instances are equal if they contain the same elements.

The Java platform contains three general-purpose Set implementations: HashSet , TreeSet , and LinkedHashSet . HashSet , which stores its elements in a hash table, is the best-performing implementation; however it makes no guarantees concerning the order of iteration. TreeSet , which stores its elements in a red-black tree, orders its elements based on their values; it is substantially slower than HashSet . LinkedHashSet , which is implemented as a hash table with a linked list running through it, orders its elements based on the order in which they were inserted into the set (insertion-order). LinkedHashSet spares its clients from the unspecified, generally chaotic ordering provided by HashSet at a cost that is only slightly higher.

Here’s a simple but useful Set idiom. Suppose you have a Collection , c , and you want to create another Collection containing the same elements but with all duplicates eliminated. The following one-liner does the trick.

It works by creating a Set (which, by definition, cannot contain duplicates), initially containing all the elements in c . It uses the standard conversion constructor described in the The Collection Interface section.

Or, if using JDK 8 or later, you could easily collect into a Set using aggregate operations:

Here’s a slightly longer example that accumulates a Collection of names into a TreeSet :

And the following is a minor variant of the first idiom that preserves the order of the original collection while removing duplicate elements:

The following is a generic method that encapsulates the preceding idiom, returning a Set of the same generic type as the one passed.

Set Interface Basic Operations

The size operation returns the number of elements in the Set (its cardinality). The isEmpty method does exactly what you think it would. The add method adds the specified element to the Set if it is not already present and returns a boolean indicating whether the element was added. Similarly, the remove method removes the specified element from the Set if it is present and returns a boolean indicating whether the element was present. The iterator method returns an Iterator over the Set .

The following program prints out all distinct words in its argument list. Two versions of this program are provided. The first uses JDK 8 aggregate operations. The second uses the for-each construct.

Using JDK 8 Aggregate Operations:

Using the for-each Construct:

Now run either version of the program.

The following output is produced:

Note that the code always refers to the Collection by its interface type ( Set ) rather than by its implementation type. This is a strongly recommended programming practice because it gives you the flexibility to change implementations merely by changing the constructor. If either of the variables used to store a collection or the parameters used to pass it around are declared to be of the Collection ‘s implementation type rather than its interface type, all such variables and parameters must be changed in order to change its implementation type.

Furthermore, there’s no guarantee that the resulting program will work. If the program uses any nonstandard operations present in the original implementation type but not in the new one, the program will fail. Referring to collections only by their interface prevents you from using any nonstandard operations.

The implementation type of the Set in the preceding example is HashSet , which makes no guarantees as to the order of the elements in the Set . If you want the program to print the word list in alphabetical order, merely change the Set ‘s implementation type from HashSet to TreeSet . Making this trivial one-line change causes the command line in the previous example to generate the following output.

Set Interface Bulk Operations

Bulk operations are particularly well suited to Set s; when applied, they perform standard set-algebraic operations. Suppose s1 and s2 are sets. Here’s what bulk operations do:

• s1.containsAll(s2) — returns true if s2 is a subset of s1 . ( s2 is a subset of s1 if set s1 contains all of the elements in s2 .)
• s1.addAll(s2) — transforms s1 into the union of s1 and s2 . (The union of two sets is the set containing all of the elements contained in either set.)
• s1.retainAll(s2) — transforms s1 into the intersection of s1 and s2 . (The intersection of two sets is the set containing only the elements common to both sets.)
• s1.removeAll(s2) — transforms s1 into the (asymmetric) set difference of s1 and s2 . (For example, the set difference of s1 minus s2 is the set containing all of the elements found in s1 but not in s2 .)

To calculate the union, intersection, or set difference of two sets nondestructively (without modifying either set), the caller must copy one set before calling the appropriate bulk operation. The following are the resulting idioms.

The implementation type of the result Set in the preceding idioms is HashSet , which is, as already mentioned, the best all-around Set implementation in the Java platform. However, any general-purpose Set implementation could be substituted.

Let’s revisit the FindDups program. Suppose you want to know which words in the argument list occur only once and which occur more than once, but you do not want any duplicates printed out repeatedly. This effect can be achieved by generating two sets — one containing every word in the argument list and the other containing only the duplicates. The words that occur only once are the set difference of these two sets, which we know how to compute. Here’s how the resulting program looks.

When run with the same argument list used earlier ( i came i saw i left ), the program yields the following output.

A less common set-algebraic operation is the symmetric set difference — the set of elements contained in either of two specified sets but not in both. The following code calculates the symmetric set difference of two sets nondestructively.

Set Interface Array Operations

The array operations don’t do anything special for Set s beyond what they do for any other Collection . These operations are described in The Collection Interface section.

Источник